Octopath Traveler is an RPG where you take control of eight characters, each having a unique job with a unique set of skills. In the course of the game you may give each character a secondary job (but you can't endow them with the same job twice). Since a party may only consist of four of these characters and it is advantageous to have access to ablities from all eight jobs, I wondered: Given a distribution of secondary jobs, is it always possible to find a party of four characters having access to all eight jobs?
It was possible for the distribution of secondary jobs I have used but in general the answer is no. To see why and to find out what kinds of distributions give rise to a favorable party required me to take a deep dive into basic abstract algebra again.
This blog post is a two-fold testimony: For one, it shows a new peak in my nerdyness and also, it shows that even after years of studying maths it is still possible to stumble upon interesting problems in very basic areas.
A gentle motivation for the symmetric group
The eight jobs in Octopath Traveler are as follows.
- Hunter
- Warrior
- Scholar
- Cleric
- Dancer
- Apothecary
- Thief
- Merchant
Choosing secondary jobs needs to follow two rules:
- No secondary job may be chosen twice.
- The secondary job must not coincide with the primary job.
Let us also agree that we actually want to endow each character with a secondary job; the game does not enforce this in any way, but it is definitely advantageous to do so. In combination with the first rule, this means that each job has to be chosen as a secondary job exactly once. To sum it up, what we want is an assignment that maps each job to a different one. This is a mathematical function that happens to be a bijection because of the first rule. The second rule makes this a special kind of bijection because it must move each element of the source. Furthermore, because we want to search for favorable assignments that leave us with a choice of a party having access to all eight jobs, the bijection becomes even more special.
Mathematical precision
To make the above thoughts mathematically precise, let us first do the common thing mathematicians do and throw away unnecessary details. For starters, let's replace the concrete job names by numbers \(1, \dotsc, 8\). Then, a distribution of secondary jobs corresponds to a certain bijection \(\{1, \dotsc, 8\} \to \{1, \dotsc, 8\}\). This means that we are looking for certain elements of the symmetric group \(S_{8}\). But why stop at 8? Let us replace 8 by an arbitrary even number \(2n\). Also, to make notation a little easier to read and write, let us define \([2n] := \{1, \dotsc, 2n\}\).
Definition. An element \(\sigma \in S_{2n}\) is bisectable if there is a subset \(B \subset [2n]\) such that \(\sigma(B) = [2n] \setminus B\).
Equivalently, we may also require that \([2n]\) is the disjoint union \(B \cup \sigma(B)\). Because \(\sigma\) induces a bijection \(B \to \sigma(B)\), we deduce that \[ 2n = |[2n]| = |B \cup \sigma(B)| = |B| + |\sigma(B)| = 2|B| \] so that \(|B| = n\) where \(|B|\) denotes the number of elements of the set \(B\).
Let's validate this abstraction by quickly turning back to Octopath Traveler: If we use a bijection \(\sigma\colon [8] \to [8]\) to assign secondary jobs to primary jobs, we will be able to build up a party of four characters having access to all eight jobs if and only if the bijection is bisectable. Indeed, if we can find such a party, the bijection needs to map their four jobs to the four other jobs so that we can use \(B\) as the set of the four primary jobs to prove that the bijection is bisectable. On the other hand, if the bijection is bisectable, choose \(B\) as in the definition above. Then, build up a party of characters having the four jobs that are elements of \(B\). Because the secondary jobs of those characters are then the elements of \(\sigma(B)\), all eight jobs are present in this party.
Some basic notations for elements of the symmetric group
Let us embark on our quest for classifying bisectable elements of the symmetric group. First, let me quickly talk about convenient notations for elements of the symmetric group. The first standard way of writing down an element is a table with two rows: The header consists of the numbers \(1, \dotsc, 2n\) and the second row consists of the images of those numbers. Here is an example for the case \(2n = 8\):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 1 | 8 | 7 |
Using this representation, we see that we need to make sure that each number \(1, \dotsc, 2n\) needs to appear in the second row exactly once. If we want to validate the rule that the secondary job must not coincide with the primary job, we can simply check that no column contains the same number twice. If we agree to keep the header always in mind, we might even reduce this representation by specifying elements using only the second row containing the values.
The cycle representation of a bijection is more efficient and describes what happens when we apply the bijection repeatedly. We start with one element and repeatedly apply the bijection to it until we return to the initial element. If we have not encountered all elements yet, we choose one of the remaining elements as the new starting point and repeat the procedure until we have encountered them all. During this process, we keep track of all the encountered elements by noting them down and putting brackets around the encountered elements when we return to the initial element. For the bijection above, say, we would start with the element \(1\), apply the bijection, obtain \(2\), and so on until we obtain \(6\) and realize that applying the bijection to it returns us to \(1\). Since we haven't encountered \(7\) yet, we do the same here and note that it gets mapped to \(8\) which then sends us back to where we started. The way we would then write this down is \[(1\ 2\ 3\ 4\ 5\ 6)(7\ 8).\]
Naturally, this also gives rise to a (directed) graph representation of an element of the symmetric group. The vertices are the numbers \(1, \dotsc, 2n\) and there is an edge from \(x\) to \(y\) if the bijection maps \(x\) to \(y\). For the example above, this yields the following.
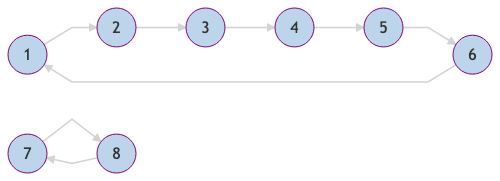
Observation. Each element of the symmetric group is the composition of disjoint cycles.
We end this section with a brief look into a basic notion of group theory that we will need when classifying bisectable elements.
Definition. The order of an element \(\sigma \in S_{2n}\) is the number of elements in the generated subgroup \(\langle\sigma\rangle := \{\sigma^i \mid i \geq 0\}\).
Lemma. Let \(\rho = (k_1\ \dotsb\ k_\ell)\) be a cycle. Then the order of \(\rho\) coincides with the length \(\ell\).
Proof. First, we show \(\rho^{\ell} = \mathrm{id}\). The cycle representation tells us precisely what happens when we apply \(\rho\) repeatedly; if we apply \(\rho\) \(\ell\) times, we move from the initial element \(\ell\) times to the right, jumping back to the beginning if necessary. Doing this to the element \(k_i\) and applying \(\rho\) \(\ell-i\) times sends us to \(k_{\ell}\). Applying \(\rho\) once more gives us \(k_1\), applying it a second time yield \(k_2\) so that applying \(\rho\) the remaining \(i\) times returns us to where we started, \(k_i\). All in all, this shows that the order is \(\leq \ell\). Second and last, we need to show that all the elements \(\rho^0, \dotsc, \rho^{\ell-1}\) are different. But this is evident since they map \(k_1\) to different elements since \(\rho^i(k_{1}) = k_{i+1}\) for \(0 \leq i \leq \ell - 1\).
Which elements are bisectable?
With cycle notation and the graph representation, we can quickly see what it means for an element to be bisectable. We need to mark half of the elements in such a way that they point at elements that are not marked. In the example of the last section, we could mark the numbers \(2, 4, 6, 8\) for example to see that the bijection is, in fact, bisectable. Here is an example of a bijection consisting of two cycles that is not bisectable:
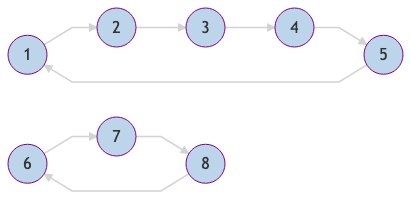
These two examples already tell the whole story.
Theorem. An element \(\sigma\) of the symmetric group \(S_{2n}\) is bisectable if and only if it is a derangement (i.e., \(\sigma(x) \neq x\) for all \(x \in [2n]\)) and is a composition of disjoint cycles of even lengths.
Proof. If we start with a derangement \(\sigma\) composed of disjoint cycles of even lengths, we may collect every other element of each cycle into a set \(B\). More precisely, let \((k_1\ \dotsb\ k_{2i})\) be a cycle of even length \(2i\). Then, select the elements \(k_2, k_4, \dotsc, k_{2i}\). Repeat this process for each of \(\sigma\)'s cycles. This way, we selected \(n\) elements that get mapped to a disjoint set \(\sigma(B)\) also containing \(n\) elements so that \([2n]\) is the disjoint union of \(B \cup \sigma(B)\).
For the other implication, I'd like to use some group theory tools, namely the orbit-stabilizer theorem, because we would have to do a quite involved argument with an odd-length cycle to derive a contradiction.
To dive into the theory of group actions, let \(\mathcal{P}([2n])\) be the set of subsets of \([2n]\) and consider the map \[ \cdot: S_{2n} \times \mathcal{P}([2n]) \to \mathcal{P}([2n]), \, (\rho, A) \mapsto (\rho \cdot A) := \rho(A). \] This is a group action which means that \(\mathrm{id} \cdot A = A\) and \(\rho \cdot (\rho' \cdot A) = \rho\rho' \cdot A\) for all subsets \(A\) and elements \(\rho, \rho'\).
We restrict this group action to the subgroup \(\langle \sigma \rangle\) generated by our given bisectable element \(\sigma\). Because \(\sigma\) is bisectable, we may choose \(B \in \mathcal{P}([2n])\) such that \(\sigma \cdot B = \sigma(B) = [2n] \setminus B\). Applying \(\sigma\) once more yields \[ \sigma^2 \cdot B = \sigma(\sigma(B)) = \sigma([2n] \setminus B) = [2n] \setminus \sigma(B) = [2n] \setminus ([2n] \setminus B) = B. \] The same equation \(\rho^2 \cdot B = B\) holds for any of \(\sigma\)'s cycles \(\rho\): If \(x \in B\) is not part of the cycle \(\rho\), we have \(\rho(x) = x\) so that \(\rho^2(x) = x \in B\). If \(x \in B\) is part of the cycle then so is \(\rho(x)\) so that \(\rho(x) = \sigma(x)\) and \(\rho^2(x) = \sigma^2(x) \in B\).
This shows that the orbit \(\langle\rho\rangle \cdot B = \{\rho^i \cdot B \mid i \geq 0\}\) consists of the two sets \(B\) and \(\rho(B)\). Now we can apply the orbit-stabilizer theorem to see that \(\rho\) must be of even length: It tells us that \[ 2|\langle\rho\rangle_B| = |\langle\rho\rangle \cdot B| |\langle\rho\rangle_B| = |\langle\rho\rangle| \] The right-hand-side coincides with the order of \(\rho\) which in turn coincides with the length. Thus, the length has to be divisible by two.
To wrap it up we still need to show that \(\sigma\) has to be a derangement. Let \(x \in [2n]\). If \(x \in B\), then \(\sigma(x) \in [2n] \setminus B\) so that \(\sigma(x) \neq x\). If \(x \in [2n] \setminus B\), then \(\sigma(x) \in \sigma^2(B) = B\) so that \(\sigma(x) \neq x\) as well and we are done.
How many elements are bisectable?
Now that we have understood precisely what kinds of elements are bisectable, we are able to count them. I've restricted myself to the case of \(2n = 8\) here. In this case, we are trying to find out how many of the 14833 derangements in total are bisectable (I won't give a derivation of that number here, but the wikipedia link contains a proof).
Let's try the following strategy. We order the bisectable elements by the lengths of their cycles. Since we know that we want to obtain a derangement consisting entirely of cycles of even lengths, this boils down to partition the number \(8\) into a sum of even numbers. Here are all possibilities: \[\begin{align*} 8 &= 8 \\ &= 6 + 2 \\ &= 4 + 4 \\ &= 4 + 2 + 2 \\ &= 2 + 2 + 2 + 2 \end{align*}\]
Counting \(8\)-cycles
Fixing elements \(k_1, \dotsc, k_{\ell}\), how many possible cycles containing those elements are there? Since the cycle representation \((k_1\ \dotsb\ k_{\ell})\) is stable under shifts, i.e., \((k_{\ell}\ k_1\ \dotsb\ k_{\ell-1})\) represents the same cycle and there are \(\ell\) different shifts, we can argue as follows. There are \(\ell!\) possibilities to write down the elements. Dividing this number by \(\ell\) accounts for the shifts. Thus, we arrive at \((\ell-1)!\) cycles.
Applying this to \(\ell = 8\), we see that there are \(7! = 5040\) different cycles of length \(8\).
Counting compositions of \(6\)- and \(2\)-cycles
First, we need to choose the \(6\) elements that belong to the \(6\)-cycle. The remaining two elements then will make up the \(2\)-cycle. There are \(\binom{8}{6} = 28\) ways to choose \(6\) elements from the \(8\) possible ones. For the resulting \(6\)-cycle there are \(5! = 120\) possibilities. Combining these, leaves us with \(28 \cdot 120 = 3360\) possibilities.
Counting compositions of two \(4\)-cycles
Again, we need to choose the \(4\) elements that belong to one of the \(4\)-cycles. There are \(\binom{8}{4} = 70\) possibilities. Next, for each of the \(4\)-cycles there are \(3! = 6\) possibilities once the elements are fixed. Last, we need to account for counting each constellation twice: For instance, the representations \((1\ 2\ 3\ 4)(5\ 6\ 7\ 8)\) and \((5\ 6\ 7\ 8)(1\ 2\ 3\ 4)\) represent the same element but we have counted it twice. Thus, we need to divide by \(2\) as a final step. This leaves us with \(70 \cdot 6 \cdot 6 / 2 = 1260\) possibilities.
Counting compositions of a \(4\)-cycle with two \(2\)-cycles.
The pattern should be clear by now:
- Choose \(4\) elements for the \(4\)-cycle. Possibilities: \(\binom{8}{4} = 70\).
- Of the remaining \(4\) elements, choose \(2\) for one of the \(2\)-cycles. Possibilties: \(\binom{4}{2} = 6\).
- For the \(4\)-cycle there are \(3! = 6\) possibilities once the elements are fixed. For the \(2\)-cycles, there is only \(1! = 1\) each.
- Account for counting each resulting element twice by dividing by \(2\).
All in all, we obtain \(1260\) possibilities.
Counting compositions of four \(2\)-cycles.
Nothing new in this computation save for the fact that we need to divide by \(4! = 24\) at the end to account for the order of the four \(2\)-cycles.
All in all, we obtain \(105\) possibilities.
Putting it all together
Summing all the possibilities, we obtain \(11025\) bisectable elements in \(S_8\). This means that the majority of the \(14833\) derangements is bisectable! More precisely, if we choose a derangement randomly we will have a probability of \(11025/14833 \sim 0.743 = 74.3\%\) of the elements being bisectable.
Some closing thoughts about choosing the bisectable element for Octopath Traveler
If we want to apply this to Octopath Traveler there will be two things to note:
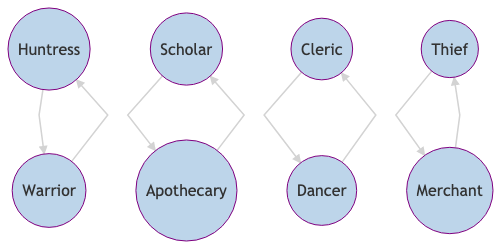
- For each cycle, there are two ways to choose which elements should belong to the bisecting set. Thus, to maximize the number of parties having access to all eight jobs, it can be favorable to only use \(2\)-cycles. Considering that the character you started with has to stay in the party for the majority of the game, this leaves you with \(8\) possible parties.
- When choosing the \(2\)-cycles, i.e., the pairs of characters that swap jobs,
it might be favorable to consider their path actions. For instance, putting
the huntress and the warrior into a \(2\)-cycle allows you to use either of
them in your party to have access to both huntress and warrior skills as well
as use their challenge or provoke path actions. Following this train of
thought leads me to the following bisectable element.